scheinbare / absolute Helligkeit
Vorab ein Versuch, die scheinbare und die absolute Helligkeit praktisch zu erklären.
Scheinbare Helligkeit:
Nimm eine handvoll unterschiedliche große Kieselsteine. Werfe ein Stein nach dem andern so weit es geht weg. Wenn Du gut geworfen hasst, dann befinden sich die Steine in unterschiedlichen Distanzen.
Nun schau hin und vergleiche. Du siehst Steine in scheinbar unterschiedlichen Größen. Doch ist der scheinbar größte Stein wirklich der Größte, oder liegt er in einer geringeren Distanz zu Dir? Was ist mit dem scheinbar kleinsten Stein, ist er vielleicht der tatsächlich größte Stein und liegt weiter entfernt?
Resultat der Geschichte: Du erkennst nur die scheinbare Größe der Steine.
Absolute Helligkeit:
Jetzt kannst Du alle Steine wieder einsammeln. Lege diese Steine in einem Halbkreis auf den Tisch. Nun haben alle Steine die gleiche Distanz zu Deinen Augen. Du erkennst die absolute Größe der Steine.
Magnitude
Der Begriff Magnitude stammt vom lateinischen Wort magnitudo und bedeutet Größe.
Wie der Meter ein Maß für die Länge ist, so ist die Magnitude in der Astronomie das Maß für die Helligkeit aller Himmelsobjekte.
Doch Vorsicht: Helligkeit ist relativ.
In der Astronomie spricht man von der scheinbaren Helligkeit und von der absoluten Helligkeit.
Die Bezeichnung Magnitude, gilt für die scheinbare und für die absolute Helligkeit gleichermaßen.
Um bei den Wertangaben zu unterscheiden, wurde folgende Schreibweise festgelegt.
Sonne - scheinbare Helligkeit: -26,8 mag oder -26m,8
Sonne - absolute Helligkeit: 4,87 Mag oder 4M,87
Die scheinbare Helligkeit
beschreibt ausschließlich nur die Lichtmenge eines Objektes, die beim Betrachter ankommt.
Zu der Grafik unten: Schauen wir zu den Sternen, so erscheinen uns diese unterschiedlich hell. Doch über die Entfernung oder Leuchtkraft der Sterne können wir keine Aussagen machen.
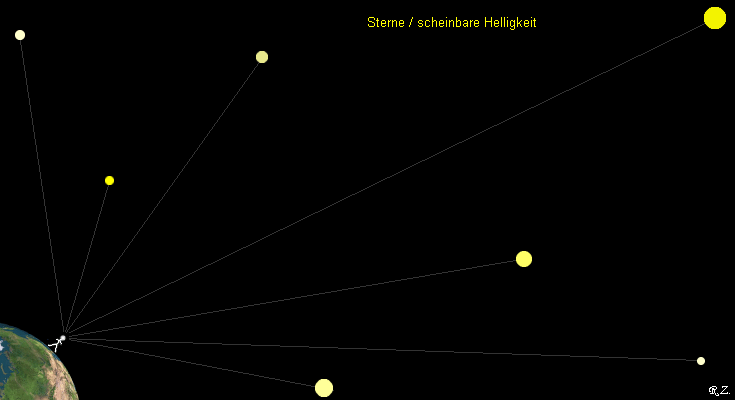
Warum benutzen wir eigentlich die "scheinbare" Helligkeit?
Nun, weil wir die Himmelsobjekte so sehen und wir Vergleiche aufstellen können. Auch bietet die scheinbare Helligkeit ein Maß, um unseren Mitmenschen etwas über gesehene Objekte mitzuteilen.
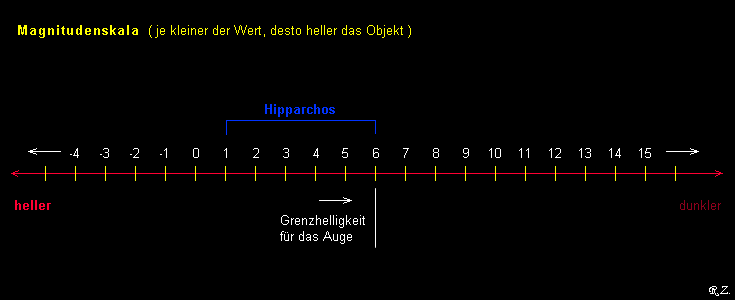
Etwa 120 v. Chr. hat der griechische Astronom Hipparchos die Idee, die Sterne zu klassifizieren.
Hipparchos teilte alle mit dem Auge sichtbare Sterne in sechs Größenklassen (Magnituden) ein.
Die hellsten Sterne erhielten die erste Größenklasse "1 mag"
Die gerade noch sichtbaren Sterne erhielten die sechste Größenklasse "6 mag"
Als im 19. Jahrhundert die Fotografie erfunden wurde, konnten die Sterne exakter klassifiziert werden. Das Grundprinzip von Hipparchos hat man beibehalten. Die Skala wurde jedoch nach unten und oben erweitert. Folglich entstanden auch negative Werte. Dieses System findet heute noch seine Anwendung.
Nun wird es noch etwas kompliziert.
Mit dem Fortschritt der Fotografie wurde auch das Fotometer entwickelt. Es ist ein Gerät um die tatsächliche Strahlungsleistung einer Lichtquelle, im (für die Augen) sichtbaren Licht zu messen.
Die Sinnesorgane der Menschen nehmen die Empfindungen logarithmisch wahr. Dies entdeckte Ernst Heinrich Weber im 19. Jahrhundert. Die Augen machen dar keine Ausnahme.
Beispiel: Schauen wir in eine Lichtquelle mit einer gemessenen Strahlungsleistung "X" und daneben in eine Lichtquelle mit 2 mal "X", so nehmen wir diese nicht doppelt so hell wahr.
So, nun gab es zwei Werteskalen. Die logarithmischen Werte und die dezimal Werte.
Messungen, zwischen einem Stern der 6. Größenklasse und einem Stern der 1. Größenklasse, ergaben die hundertfache Leuchtkraft.
Mitte des 19. Jahrhunderts wurde folgende Umrechnung festgelegt.
Fakt war nun, dass zwischen Sternen mit 1 mag, und 6 mag, ein Unterschied von fünf Größenklassen besteht. Dieser Unterschied beträgt die 100 fache gemessene Leuchtkraft.
So wurde die 5. Wurzel von 100 genommen. Resultat: 2,5118864315095801110850320677993
Mit diesem Resultat lassen sich nun die logarithmischen Werte (Größenklassen) in Dezimalwerte (gemessene Leuchtkraft) umrechnen.
Größenklassendifferenzen = 2,512 x 2,512 = 6,3 x 2,512 = 15,9 x 2,512 = 39,8 u.s.w.
Siehe auch folgende Grafiken.
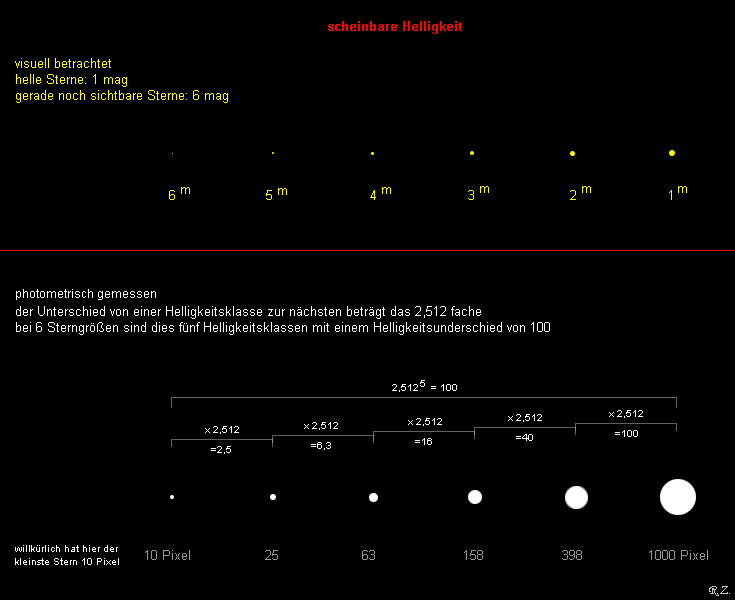
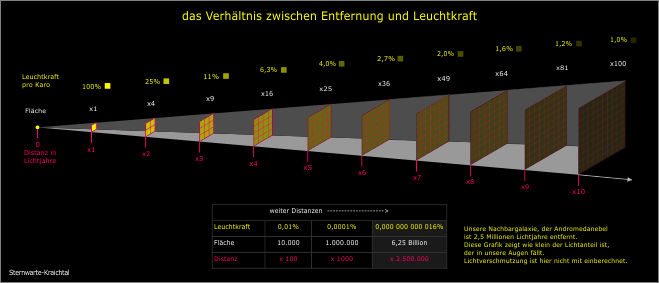
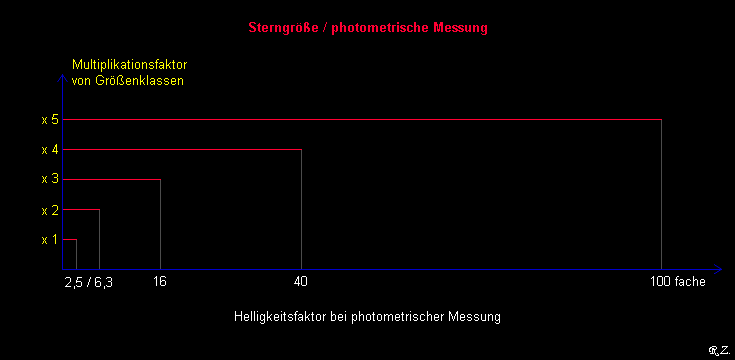
Die folgende Grafik soll noch einmal verdeutlichen wie die Schere zwischen den Größenklassen und der fotometrischen Messung auseinander geht.
Übrigens, kann das Weltraumteleskop Hubble Himmelsobjekte bis 31 mag erkennen. Wenn wir das mit einem Stern von 6 mag (mit dem Auge gerade noch sichtbar) vergleichen, so entspricht das einer Differenz von 25 Größenklassen. Was einen tatsächlichen Helligkeitsunterschied von über 10 Milliarden ergibt.
Das Bedeutet, dass Hubble Objekte aufspüren kann, die 10.000.000.000-mal schwächer leuchten, als die Objekte, die wir mit dem bloßen Auge gerade noch sehen können.
Die absolute Helligkeit
ist ein Maß für Himmelsobjekte, in einer gedachten Distanz von 10 parsec. (1parsec = 3,26 Lichtjahre)
Die Größenangaben bei der "scheinbaren Helligkeit" besagen, wie hell wir die Himmelsobjekte sehen.
Um jedoch die wahren Leuchtkräfte der Objekte miteinander vergleichen zu können, benötigen wir einen gemeinsamen Nenner. Dieser ist eine gedachte Position in einer Entfernung von 10 parsec.
Versetzen wir zum Beispiel die Sonne, den sehr hell leuchtenden Stern Sirius, den Polarstern und den Stern Rigel auf diese Linie.
| Sterne | Entfernung | scheinbare Helligkeit |
absolute Helligkeit (bei 10 parsec) |
Differenz zur Sonne |
Helligkeitsunter- schied zur Sonne |
| Sonne | 150.000.000 km | -26m,8 | 4M,84 | --- |
--- |
| Sirius | 8,6 Lichtjahre | -1m,4 | 1M,45 | 3M,39 | 23 |
| Polarstern | 431 Lichtjahre | 2m,0 | -3M,64 | 8M,48 | 2.466 |
| Rigel | 770 Lichtjahre | 0m,2 | -6M,69 | 11M,53 | 40.926 |
Folgende Grafik soll das oben beschriebene verdeutlichen.
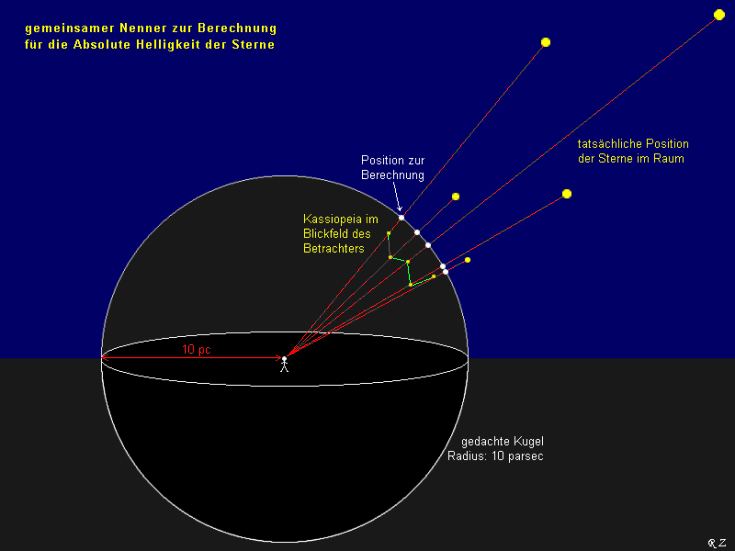
Die Leuchtkraft nimmt mit der Entfernung im Quadrat ab.
Wie verhält sich die Leuchtkraft zur Entfernung des Betrachters?
Oder warum leuchten Sterne so schwach, dass wir Teleskope benötigen, um sie zu sehen?
Praktische Beispiele:
Jeder, der schon einmal in der Kälte an einem Lagerfeuer stand, weiß wie groß die Hitze in der Nähe ist. Doch geht man nur ein oder zwei Schritte zurück, nimmt die Strahlungswärme gewaltig ab.
Viele Autofahrer kennen das Phänomen geblendet zu werden. Kommt ein Fahrzeug entgegen, so nimmt die Helligkeit der Scheinwerfer gewaltig zu. Die Ursache aber liegt nicht daran, dass die Scheinwerfer auf einmal mehr Energie abstrahlen.
Ein Stern strahlt seine Energie in alle Richtungen ab.
Versetzen wir nun einen Stern in die Mitte einer gedachten Kugel.
Bezeichnen wir den Radius der Kugel mit r1
und die daraus errechnete Kugeloberfläche mit x1
Nehmen wir an, die abgestrahlte Energie von dem Stern hätte bei der Kugeloberfläche den Wert E100
Vergrößern wir nun die Kugel um den doppelten Radius r2
hierbei vervierfacht sich die Kugeloberfläche x4
Nun, die Energie wird ja nicht mehr, doch die bestrahlte Fläche hat mit dem Faktor 4 zugenommen.
Folglich hat die Strahlungsintensität pro Quadrat abgenommen. Der Wert beträgt nun E 25
Fakt ist:
Bei Verdopplung eines Kugelradius nimmt die Kugeloberfläche stets im Quadrat zu und die Leuchtkraft nimmt im Quadrat ab.
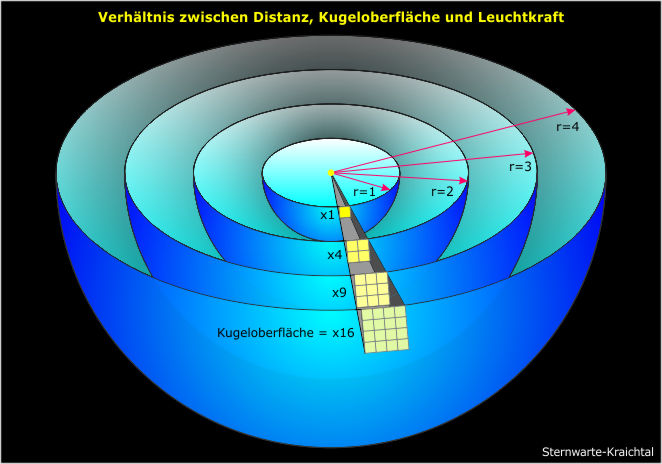
Die folgenden Grafiken sollen das noch einmal verdeutlichen. Anmerkung: Jedes einzelne Karo hat die gleiche Größe.
Ich denke, dass diese letzte Grafik das Verhältnis zwischen Distanz, Kugeloberfläche und Leuchtkraft schön verdeutlicht.
2004 / 2016 Roland Zimmermann